关于离散元接触力组构分析的讨论

Introduction

所谓接触力组构分析（Analysis of Fabric Anisotropy），就是分析颗粒体系间法向、切向接触力的作用方向，研究力的传递规律，是研究细观介质的一个重要手段，可参考Rothenburg ^[1] 接触力分布函数相关内容。

图1 接触力组构分析示意图

二维案例

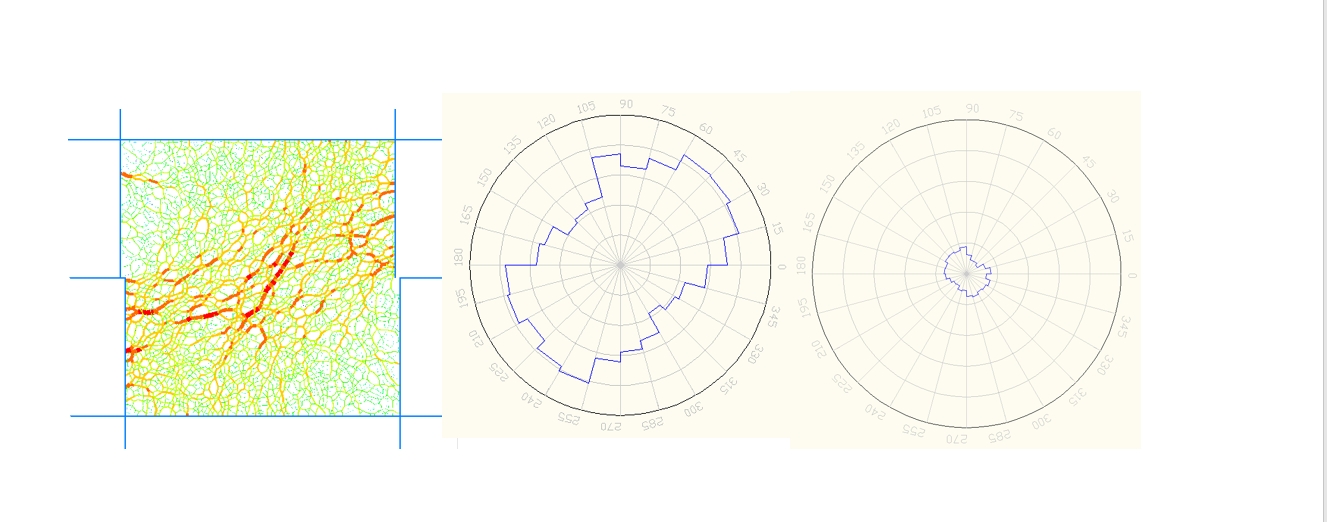
二维的情况就比较简单了，每两个颗粒间的接触力可以分为法向力和切向力，PFC中可以通过内置的FISH函数导出接触力的单位方向向量(contact.shear/contact.normal)以及力的模(contact.force.shear/contact.force.normal)。但是值得注意的是法向力的模是具有正负号的，用于标识法向力为拉力还是压力。二维案列的玫瑰花图绘制的原理就是将平面空间的方位划分成一系列方位子区间，然后统计接触力在这些区间的分布特征。以图1为例，就是将360度的方位分布以15度为一个区间进行分区，按照接触力的方向单位向量将接触划分到所属的子方位分区，最后统计该区间包含的所有接触力。对于某个单位向量(x,y)，计算其所属的区间只需要计算degree=arctan(y/x)即可。

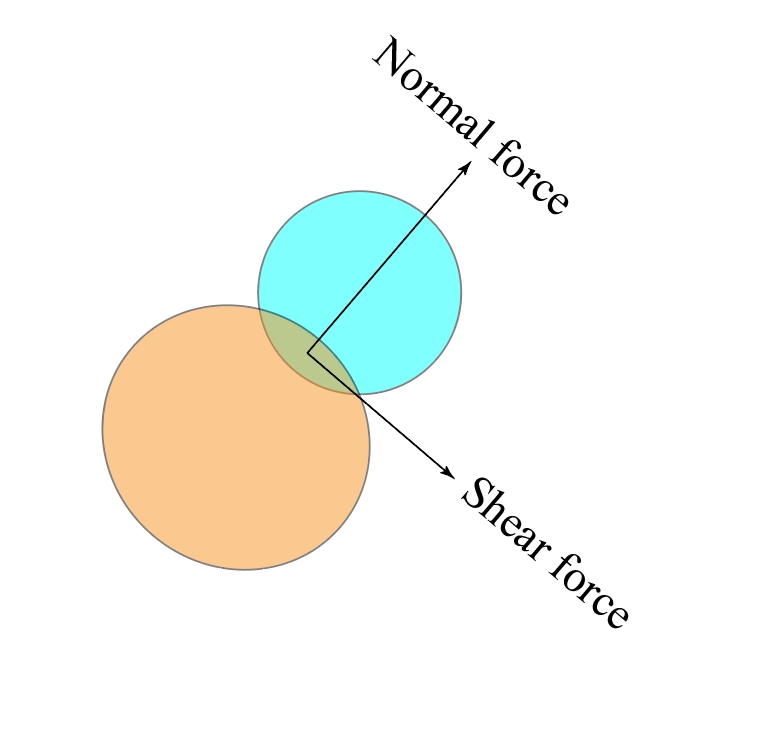
对力具体所属的区间进行划分后，下一步我们需要确定的就是如何统计各区间内包含的接触力。第一个需要考虑的问题就是对区间包含的力是计算平均值还是求和值。笔者目前没有在网上找到关于接触力统计的开源代码实现，自编程序的实现只能根据已有的论文资料以及石崇老师在书籍《颗粒流（PFC5.0）数值模拟技术及应用》中的配套程序进行反推。论文^[2]中， 给出了双轴试验接触力统计结果的拟合公式，见下式。简单来说，就是对画出来的玫瑰花图的轮廓用函数进行描述。其中f₀这个系数的量级到了10⁵至10⁶，而辅助分析小程序/6-组构分析-石/pfc_contact_information.dat的数据显示两颗粒间接触力的量级大约为几百到几千。因此，第一个推论为每个方位子区间统计的模式是计算所有包含接触力的求和值。第二个值得讨论的问题为展示法向力时，求和是有符号求和还是对绝对值求和。根据图1给出的展示以及石崇在辅助分析小程序/6-组构分析-石中给出的展示结果，并未观察到玫瑰花图径向数值有负值的存在。因此第二个推论为统计方位子区间的求和值之前需要对每个力的模量取绝对值。

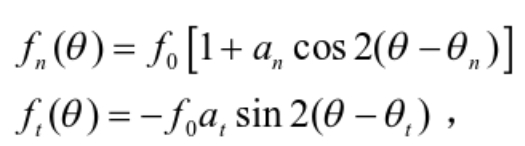
理论介绍结束，实践验证开始。将辅助分析小程序/6-组构分析-石文件夹中的pfc_contact_information.dat文件在基于上述理论编写的Python代码进行验证，并同石崇plot_rose_picture_2D.exe程序的结果进行对比。切向力与法向力比较结果如下，左图为石崇plot_rose_picture_2D.exe的结果，结果接近，但存在差异，哪里存在问题？大家不必在意图形的大小问题，因为石崇径向半径的比例尺是固定值，笔者程序径向半径比例尺为自适应调整。

切向力结果比对

法向力结果比对 为了找到问题所在，笔者又将某个二维单轴压缩模型的接触力信息导出并绘制玫瑰花图，比对结果如下：

切向力结果比对

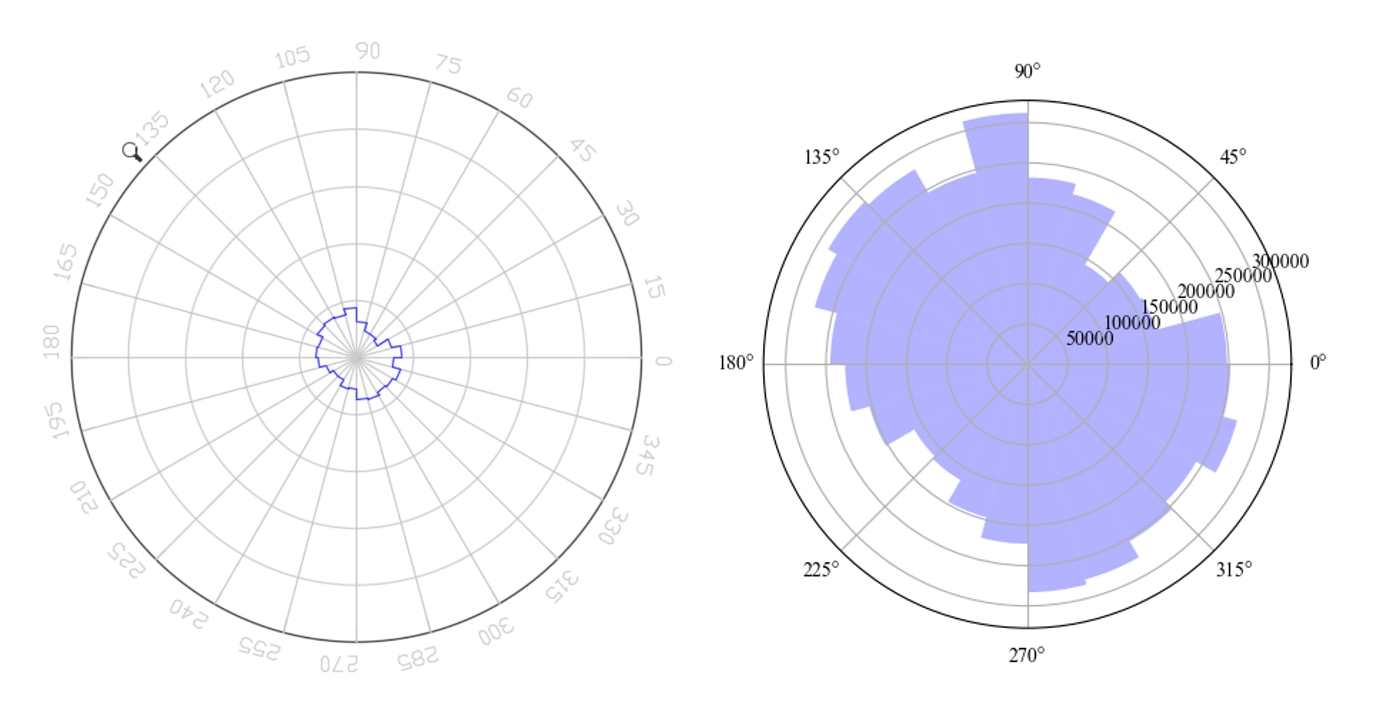
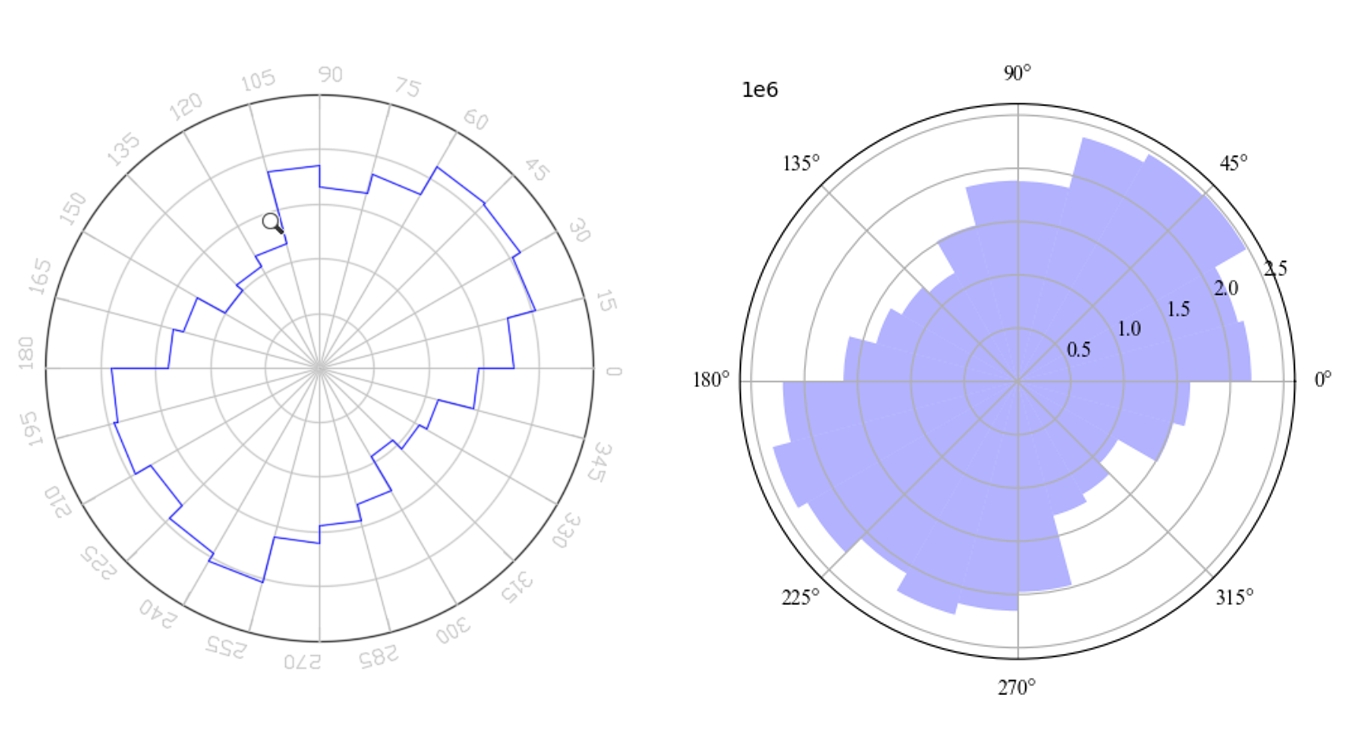
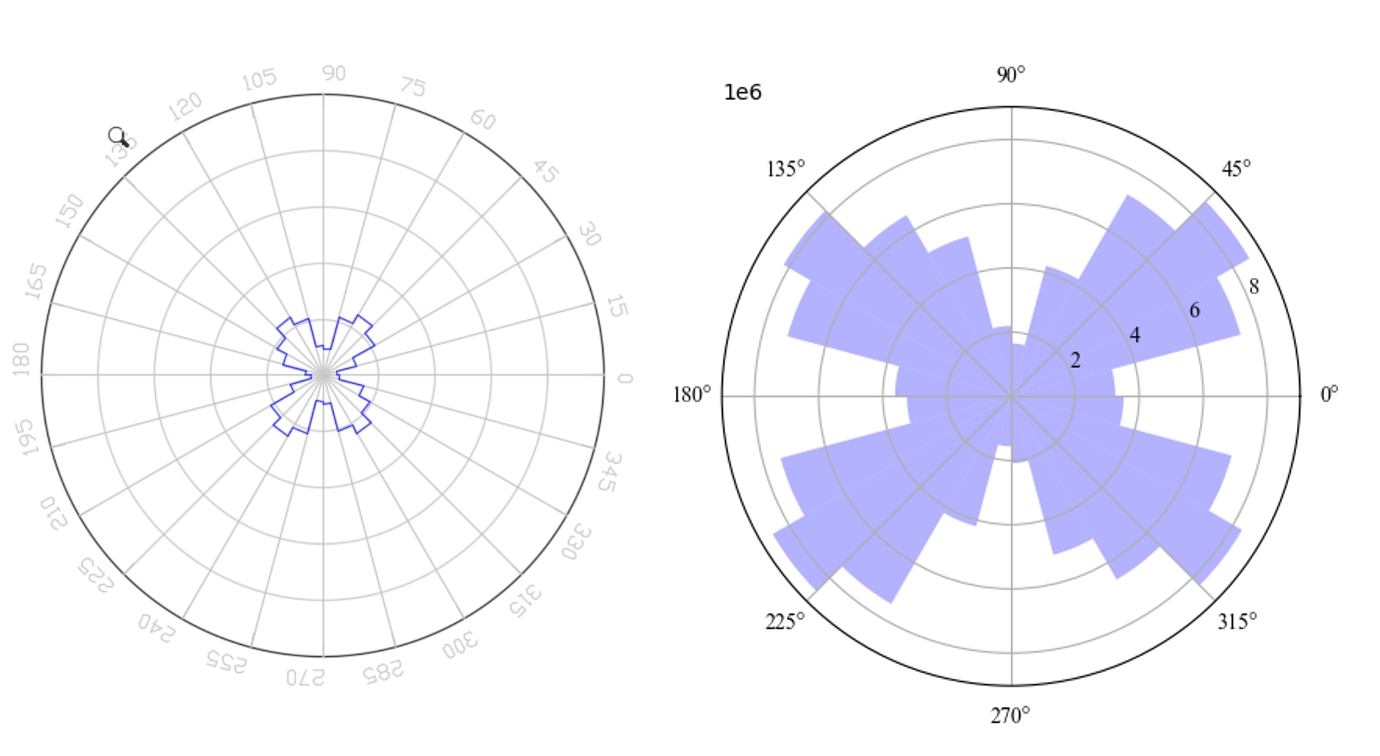
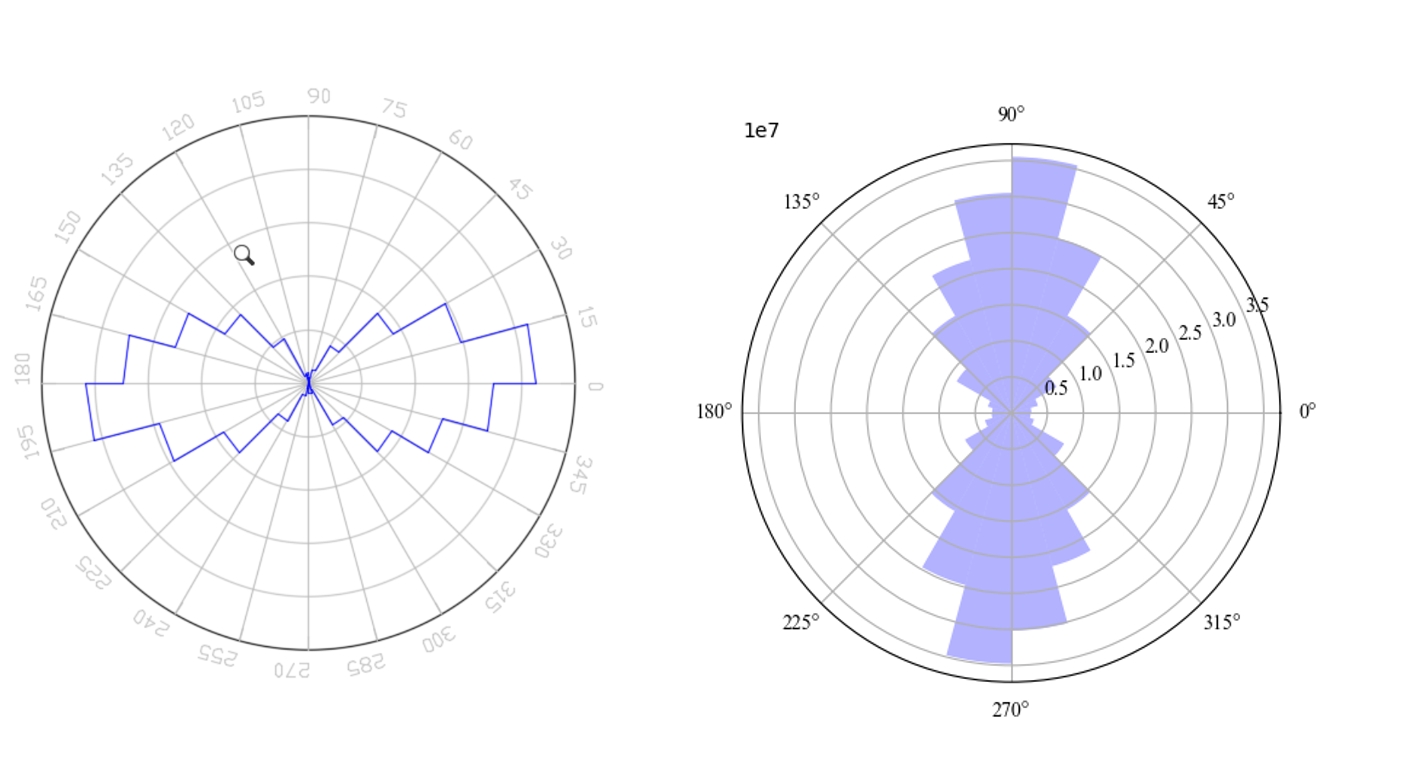
法向力结果比对 这样看的话，将石崇的图形旋转90度才能和笔者程序的图对应上。笔者推断自编程序和石崇程序对于接触力的方位区间划分存在差异，那么存在差异的话，石崇程序可能是如何编写？孰对孰错？但是从文献^[1,2]中对于法向力的展示结果来看，单轴、双轴试验的法向力玫瑰花图都是竖着的而不是横着的。难道网上公布的这个辅助分析小程序/6-组构分析-石/plot_rose_picture_2D.exe程序是个错误的版本？

文献2中法向力的玫瑰花图结果

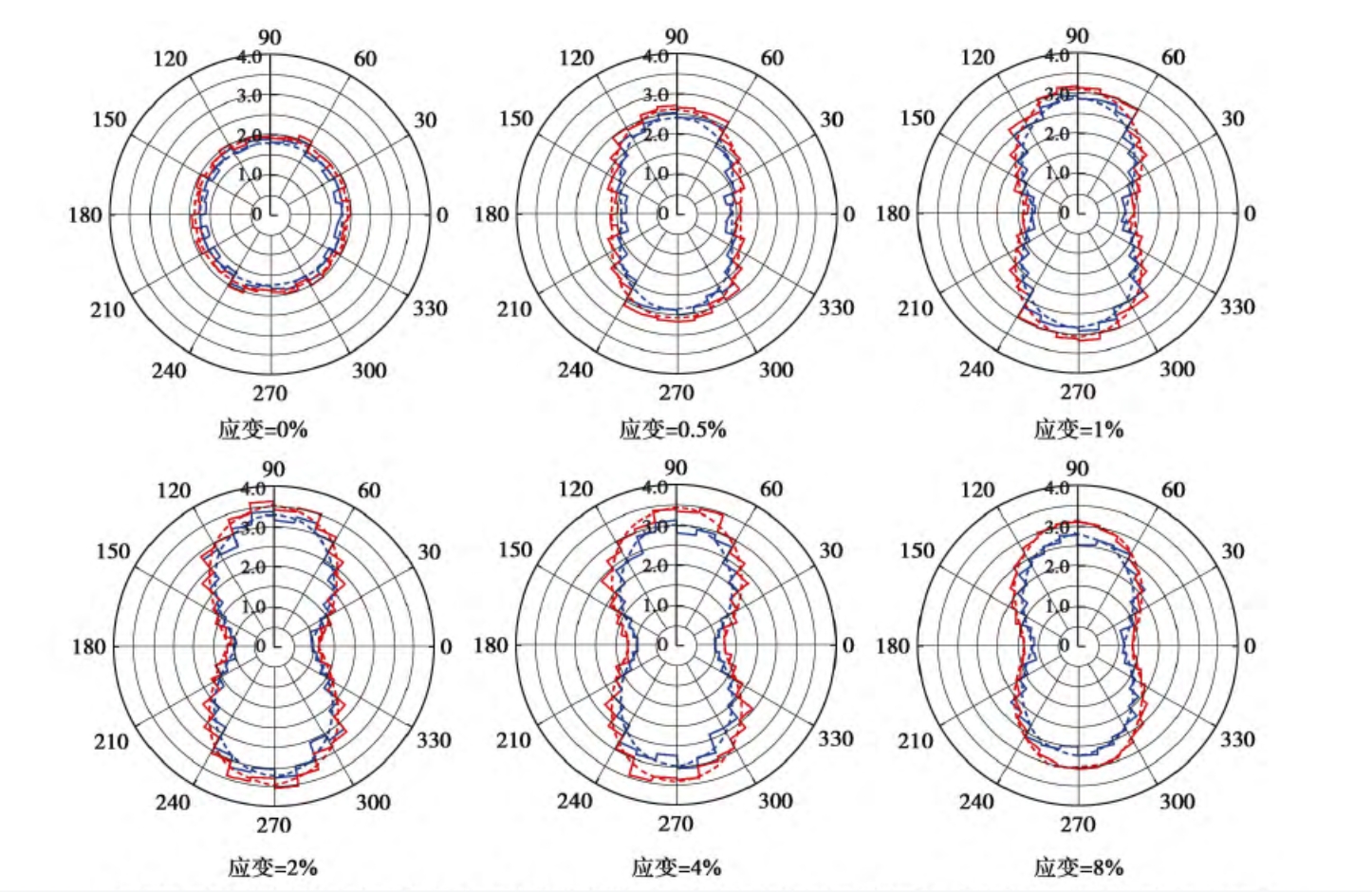
三维案例

三维模型的二维可视化展示

对于三维离散元模型而言，二维的可视化展示就是继续用上面的二维玫瑰花图展示三维的接触力。石崇在辅助分析小程序\6-2三维直接剪切xoz面组构分析-石\三维直接剪切xoz面组构图分布.exe中给出了三维直剪案例的二维可视化程序。字面意思上理解，似乎是对于接触力的三维方向单位向量(x,y,z)，直接舍弃掉y分量，然后通过arctan(z/x)来计算接触力所属的方位子区间。直觉上理解，就是把三维空间沿着y轴投影到XOZ平面上，默认情况下，XOZ的假定如下图所示。暂且这么假定，让我们看看结果。

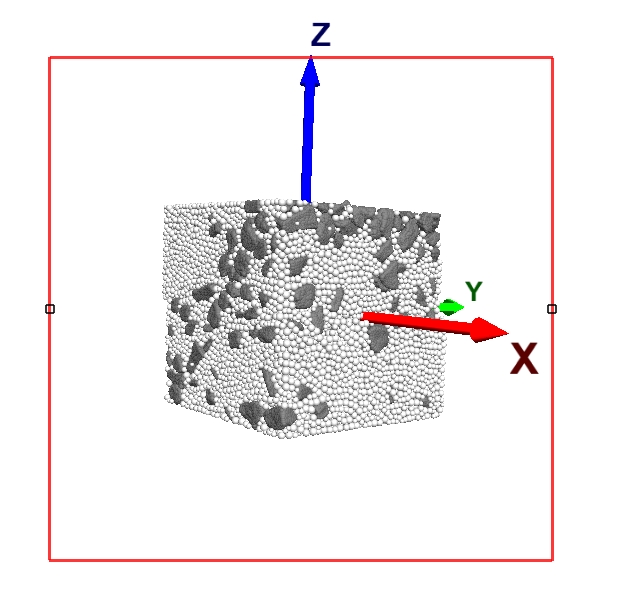
y分量丢弃方案

首先可以看到 辅助分析小程序\6-2三维直接剪切xoz面组构分析-石文件夹下，用于示范的pfc_contact_information.dat文件每行只有9个数据，而如果按照辅助分析小程序\6-2三维直接剪切xoz面组构分析-石\导出接触信息命令流PFC3D5.0.txt中的代码（下示代码），导出的数据每行应该具有12个数据。点击运行三维直接剪切xoz面组构图分布.exe，每行9个数据的文件报错，也就是说这里文件夹本身包含的示范文件有错误，应该要按照下示代码导出每行12个数据的接触信息文件。

contact_info(count)= string(contact.id(cp))+' '+string(contact.pos.x(cp))+'  ' + string(contact.pos.y(cp)) +'  ' + string(contact.pos.z(cp)) 
contact_info(count)=contact_info(count)+' ' +string(contact.normal.x(cp))+' ' +string(contact.normal.y(cp))+' ' +string(contact.normal.z(cp))         
contact_info(count)=contact_info(count)+' ' +string(contact.shear.x(cp))+' ' +string(contact.shear.y(cp))+' ' +string(contact.shear.z(cp))
contact_info(count)=contact_info(count)+' ' +string(contact.force.normal(cp))+' ' +string(contact.force.shear(cp))

因此，笔者又导出了某个三维单轴压缩模型的接触力信息文件，用于推测这个绘制XOZ面组构玫瑰花图程序的实现方式。下面是石崇程序的结果：

石崇程序XOZ面组构分析结果 单论法向力而言，主要分布方向还是水平的，什么问题？

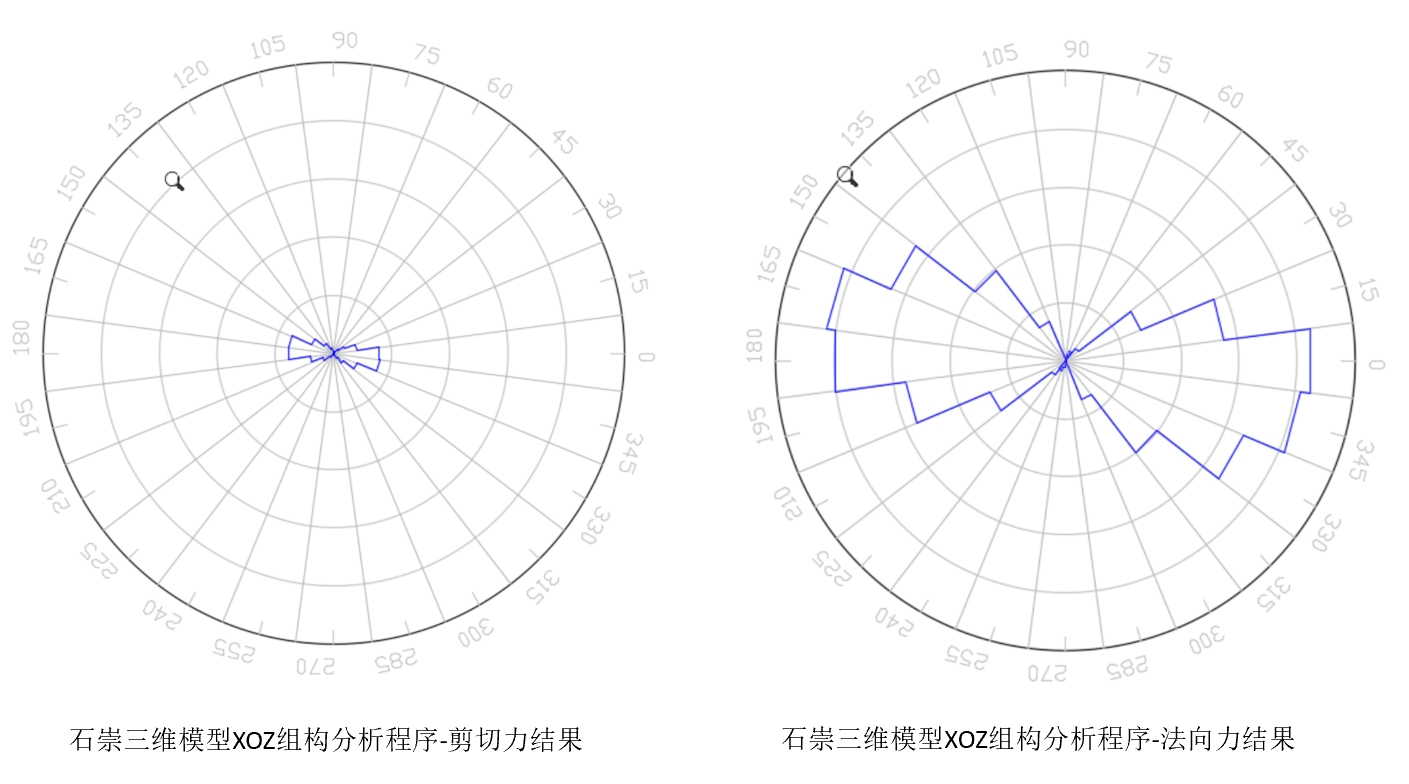
根据舍弃y分量方案，笔者给出了自己的实现结果：

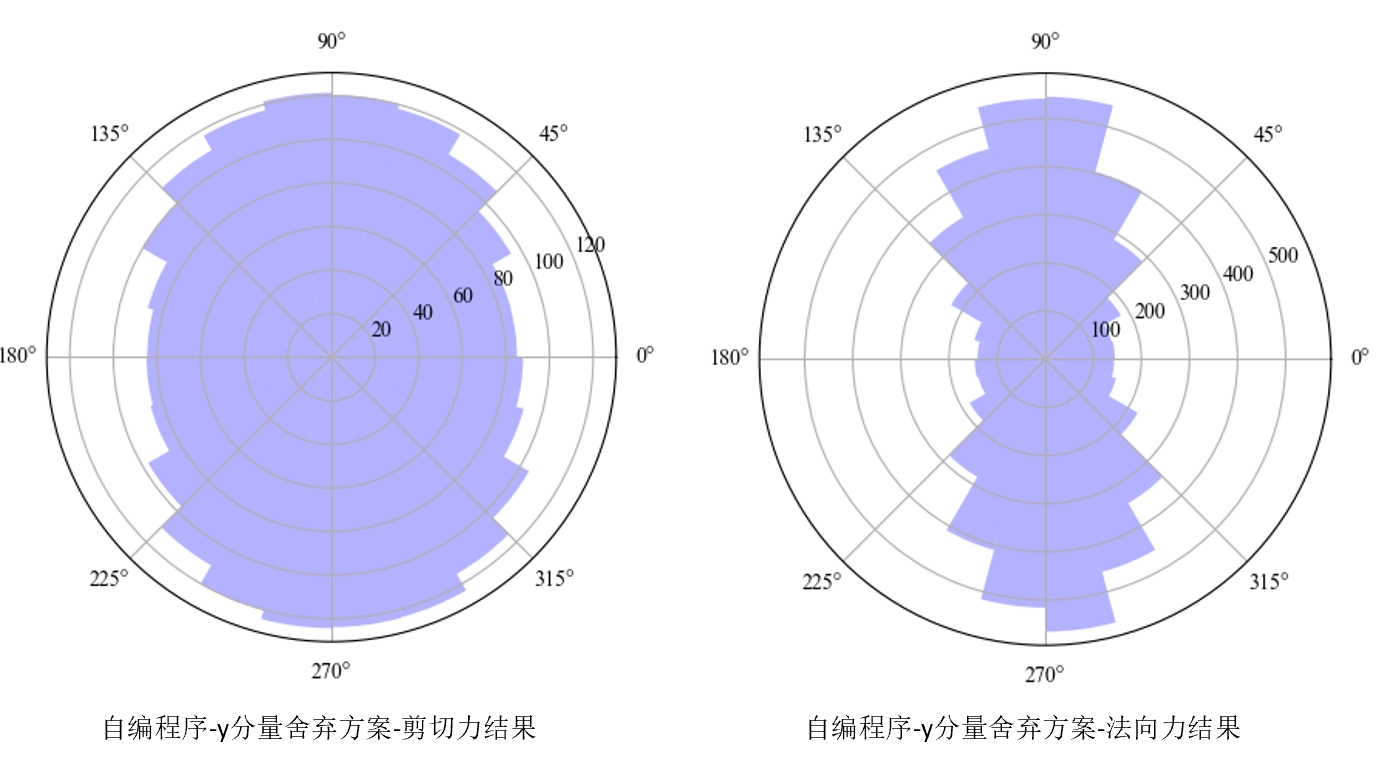
自编程序-y分量舍弃方案分析结果 我们可以看到对于玫瑰花图存在向90度以及270度聚集的异常，这是可以预见的，由于y分量的舍弃，计算接触力方位的子区间（等价于计算方向向量的倾角）公式由arctan(z/sqrt(x2+y2))变成了arctan(z/x)，如果y分量的值较大，那么使用arctan(z/x)计算的结果也会变大，即统计结果向90度和270度聚集。

方向向量旋转方案

既然直接舍弃y分量，会使得分区的统计结果向90度和270聚集，那么就依据接触力方向向量的倾角划分，并且结合x分量的正负值决定该方向向量归属于XOZ面的X正半轴还是X负半轴，直觉上理解就是将接触力依据X分量的正负旋转到XOZ平面上，然后对接触力进行统计，结果如下：

自编程序-旋转方案分析结果

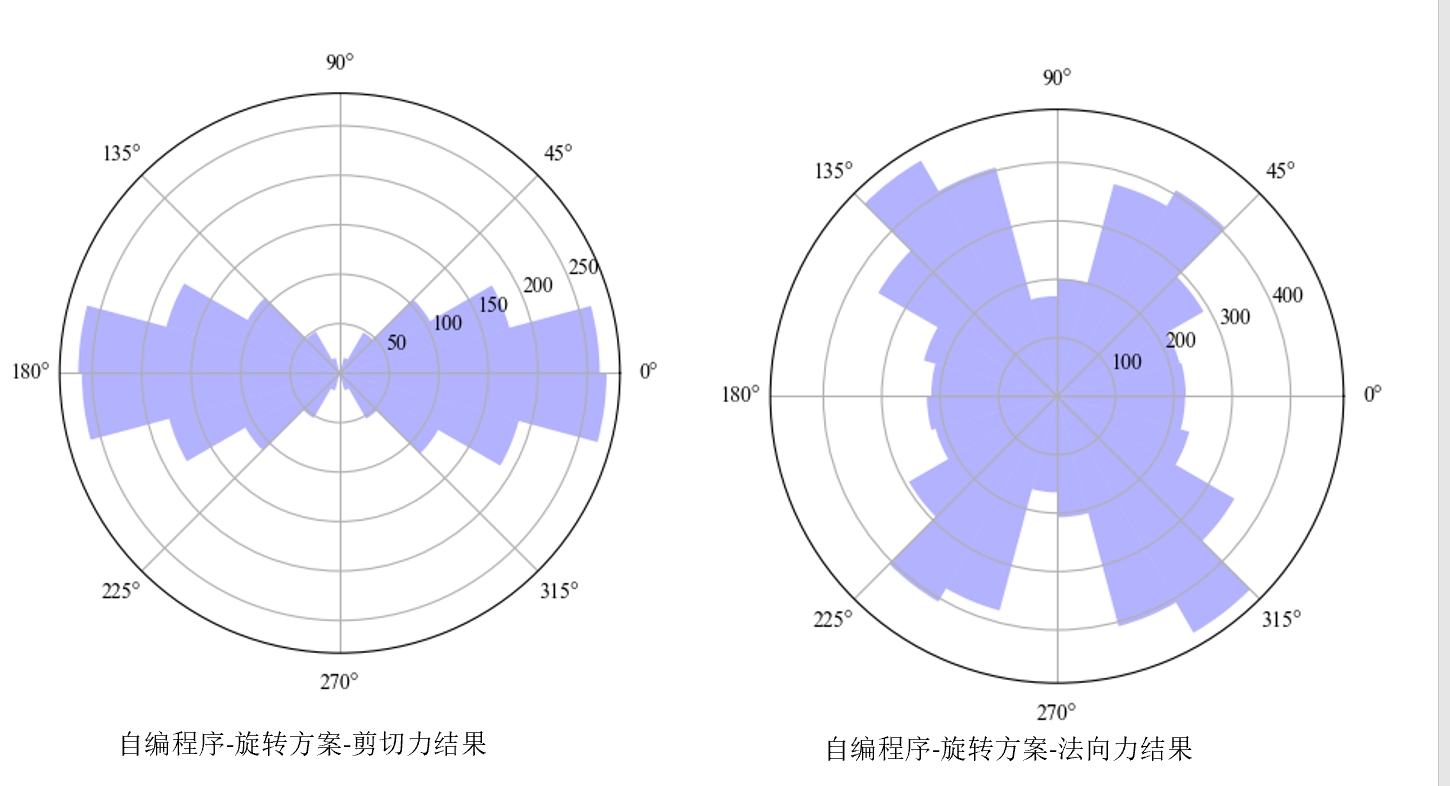
讨论

似乎上面两种方案由于信息的压缩呈现结果都不太完美，大家觉得哪种用于论文更合理？或者是否存在更佳的三维模型二维化展示方案？

三维模型的三维可视化展示

即用三维图形来展示三维的接触力，理论上可以把一个球面进行分区，然后在每个分区上绘制统计结果的柱状图。然而目前笔者还没有很好的思路做到这一点，欢迎大家交流讨论。

References

[1] ROTHENBURG L, BATHURST R J. Analytical study of induced anisotropy in idealized granular materials[J]. Géotechnique, 1989, 39(4): 601–614.

[2] 张强,汪小刚,赵宇飞,刘立鹏，林兴超，石崇.不同围压加载方式下土石混合体变形破坏机制颗粒流模拟研究[J].岩土工程学报, 2018, 40(11):10.DOI:10.11779/CJGE201811011.